Результаты стали точнее
Известный российский математик Ярослав Сергеев решил проблему неопределенности, создав новую систему счисления. Дело в том, что в области точных наук ученым нередко приходится работать с бесконечно большими и бесконечно малыми числами. Ранее для них использовались символьные обозначения, в частности знак ∞, и в итоге полученные результаты были верными, но не вполне точными. Новый подход позволяет получать численные ответы при выполнении операций с бесконечностью.

Ярослав Сергеев
Давным-давно для записи чисел люди использовали небольшой набор символов, а иногда и просто палочки. Эти символы и их группы называют нумералы: например, 10 и Х — это два разных нумерала, выражающих одно и то же число в арабской и римской системах записи.
Некоторые народы до сих пор используют простейшие системы записи чисел. Например, племя пираха, живущее в Амазонии, применяет очень простую систему нумералов: один, два, много. Пираха не знают чисел больше двух, и у них такие операции, как 2+1 и 2+2, дают одинаковый результат, то есть “много”. Они не в состоянии различать числа 3 и 4, не могут выполнять арифметические операции c ними и в целом не в состоянии сказать что-либо об этих числах, поскольку в их языке нет ни слов, ни концепций для этого.
Уровень сложности математических операций в разных цивилизациях рос постепенно. Народы создавали свои системы записи, в которых большие числа можно было написать с помощью одного или нескольких относительно простых символов. Огромным прорывом в математике стало “изобретение” ноля, а затем и возникновение степенной записи. А теперь нам не надо даже рисовать ноли, чтобы обозначить миллиард, мы просто пишем 109.

Написание числа 1000 в разных древних системах счисления
А что делать с числами, которым, на первый взгляд, невозможно дать определение? Бесконечно большие и бесконечно малые — как написать то, что сложно принять? Мы окружены предметами, у которых есть контуры, поэтому при попытках понять отсутствие границ наш мозг буквально зависает.
Традиционный взгляд на концепцию бесконечности можно описать так. Предположим, некий жадный человек отделяет от пирога огромный кусок. Но как этот жмот ни старается, все равно его кусок оказывается меньше целого пирога. А вот если бы выпечка обладала “бесконечным” размером, закон “кусок меньше целого” действовать бы перестал. Это трудно представить, но наш жадина умудрился бы отрезать себе часть, равную по размерам нетронутому пирогу! Таким образом, при выполнении действий с бесконечностью большинство привычных математических операций перестает работать.
Долгое время для обозначения бесконечности ученые пользовались символом ∞, что причиняло неудобства при исследованиях в высшей математике. Но предложенная Ярославом Сергеевым новая методология позволяет вычислить у определенных бесконечных множеств число их элементов — то есть кусков рассматриваемого пирога. Прежде всего Сергеев предложил исключить из используемых нумералов символ ∞, традиционно применяемый для представления бесконечности, и ввел вместо этого гроссуан (большую единицу, ①).
С помощью новой методологии можно определить, что количество четных натуральных чисел равно ①/2, нечетных натуральных чисел — ①/2, всех натуральных чисел — ①, а целых чисел — 2①+1. Если мы из множества целых чисел исключим ноль, то количество оставшихся чисел будет равно 2①. Тогда можно начать оперировать с бесконечностью и рассчитать число элементов с точностью до одного у определенных множеств.
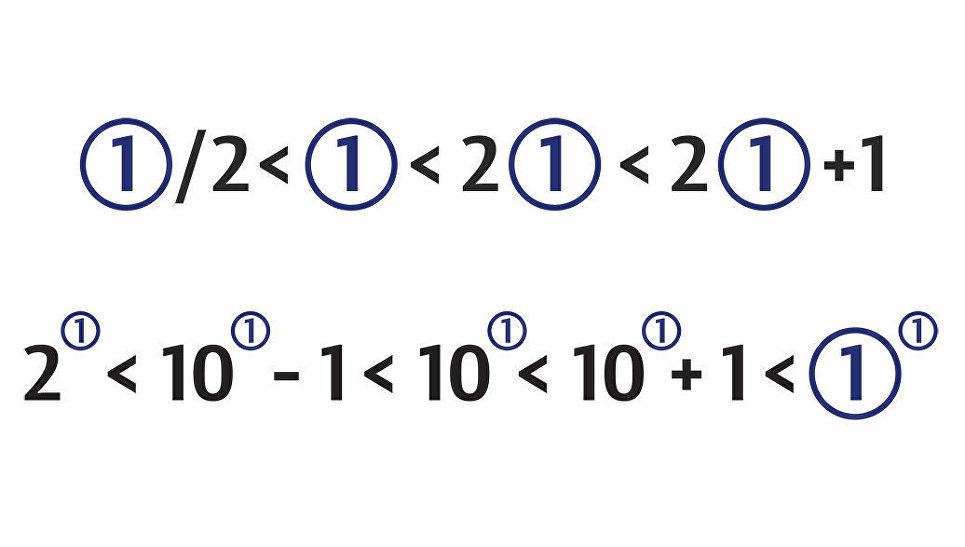
Операции с гроссуаном
“При этом введение ① позволяет построить математический анализ, в котором не появляются неопределенные формы вида ∞-∞, ∞/∞, 0*∞. Как следствие, бесконечные ряды становятся суммами с бесконечным числом слагаемых n, где значение n определяется в зависимости от решаемой задачи (например, ①/2, 3①, ①2-1), как это происходит и для конечных n”, — рассказывает Ярослав Сергеев.
За ряд открытий в математике Ярослава Сергеева наградили престижными международными премиями, в том числе “Аль-Хорезми”-2016 и премией международного конгресса World Congress in Computer Science, Computer Engineering, and Applied Computing в 2015 году.
Однако некоторые ученые активно критикуют работы Ярослава Сергеева. В частности, они осуждают оперирование гроссуаном как самым большим натуральным числом. Доктор физико-математических наук Семен Кутателадзе полагает, что “компьютер бесконечности” ничего не считает. Свою точку зрения математик аргументирует тем, что в каждом компьютере (но не истинном математическом множестве) хранится конечный набор символов, один из которых объявляется при расчетах самым большим. И можно потом организовать вычисления, использующие это символическое число, но к работе с настоящей бесконечностью подобные вычисления отношения не имеют.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.







Сообщить об опечатке
Текст, который будет отправлен нашим редакторам: